How to Unlock the Language of Math for Your Students

I’d like to take you on another journey along the road of the language of mathematics with a stop at the intersection of “math concepts and symbolic notations.”

Sometimes the mathematics conversation is just as confusing to students as this collection of signs is to a driver in an unfamiliar situation. There appears to be a variety of symbols used to identify the different types of roads in the area, just as we have a variety of concepts, operations, and relations that are conveyed through symbolic notations. 

To further complicate the issue, in math we sometimes have a variety of symbols used to convey the same concept or idea. Imagine the student’s dismay when he or she is not familiar with a new symbolic notation that is being used but is familiar (and perhaps proficient) with a different notation. This can certainly be a blow to some students’ math confidence.

Welcome back to those who have been following the conversation about how to unlock the language of math for students. Let’s explore some of the challenges with mathematical words that have more than one symbolic representation.

1. Multiplication

Multiplication is a simple word, yet we can convey the idea of multiplying using a variety of symbolic notations. Consider the phrase “the product of 12 and 9.” The phrase looks completely harmless at first. However, we can translate this as 12 x 9 or 12•9 or 12(9). To further complicate things, we will eventually place more emphasis on the use of variables. So, we move to “the product of 12 and a number, where h represents the number,” which could be represented as 12 x h or 12•h or 12(h) or 12h. And don’t forget the conversation about the commutative property, which will allow me to “switch” the order of the factors and yield the same result but a different model if I were creating a visual or concrete model. Consider an array for 12 x 9. You will create 12 rows and 9 columns, but for 9 x 12 you will create 9 rows and 12 columns.

2. Division

Division is another mathematical concept with a variety of symbolic representations. Consider 5 divided by 2. Five is the dividend, 2 is the divisor, and we have 3 different ways to write the expression.

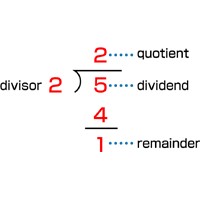
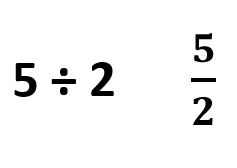
Five divided by 2 is further complicated by the directionality of the reading. In the United States, we read our sentences and most of our printed information from left to right. So the correct reading of 5 ÷ 2 is easily mastered. But when the division is represented using the division radical, shown at left above, students often misread because they are still employing a left to right direction of reading where they now need to switch to the right to left reading direction. Finally, after years of these two familiar representations, we transition to the vertical representation, shown at right above, when our emphasis is on algebraic representations.

Well, there was certainly no surprise there, right? But when we do not push pause, and make sure that students understand all the representations used in previous years before we transition to a new representation, we take a risk of leaving some students caught in a dilemma regarding how to read the situation. Sometimes they can successfully navigate their way to the correct reading and understanding, but there are also those who are unsuccessful. If left unidentified, these simple misreadings and misinterpretations become larger issues in a formal algebra program of study. And remember, the directionality of the reading is a critical key to success as well; memorization of symbols is not enough.

3. Congruency

Let’s take a look at one additional mathematical concept that has multiple symbolic notations: congruency. When we think of the word congruent, we immediately think of this symbol: ≅

But when used in context, we often use other notations—the tick marks and arcs. Consider this visual:

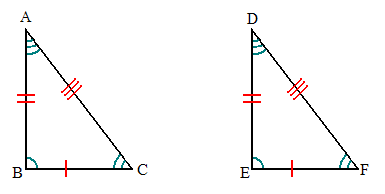The tick marks indicate which sides are congruent, and the arcs identify the congruent angles. A student may have memorized the definition for congruent but may not know how to “read” the visual if attention has not been paid to the notations that support the idea of congruency in mathematics.

In wrapping up this conversation, I would like to take you further down the math road to the intersection of “symbols we use that have one meaning in math and a different meaning outside of math.” Review the following table for a few examples:

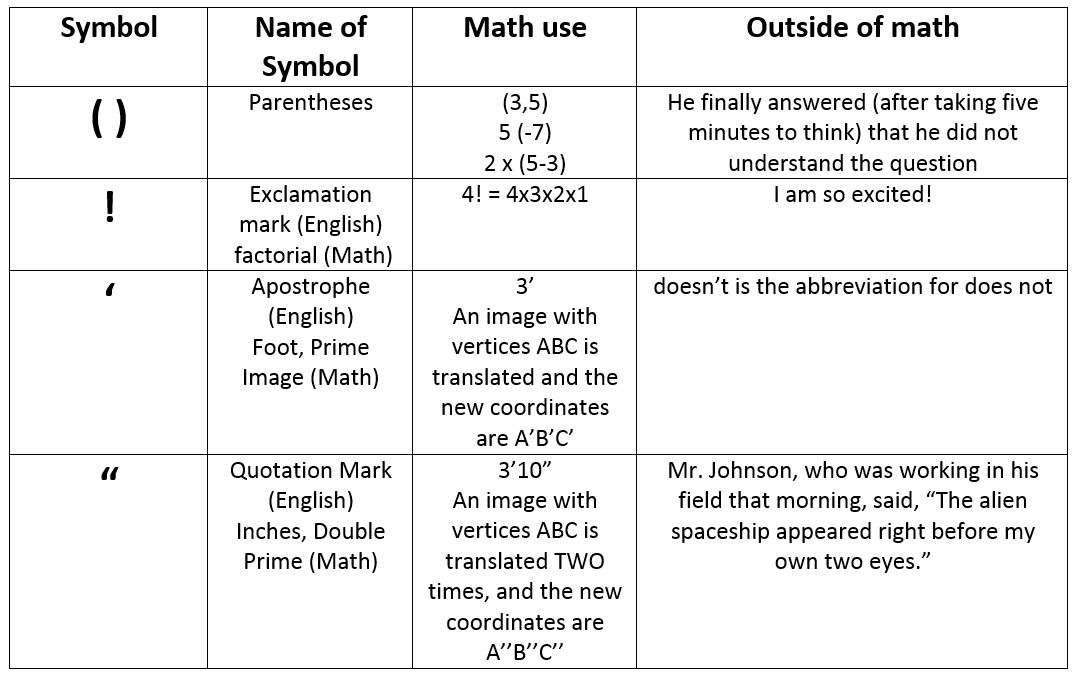
As you can see, the road to understanding the language of math can easily be a bumpy one if we do not push pause and make sure the language is understood.