It’s Time to Update Our Algorithm

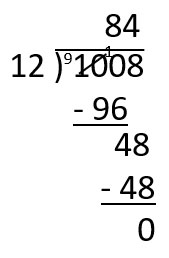
Unfortunately, we all remember this. Whether you graduated from high school two years ago or 60 years ago, somewhere in late elementary school you had togrind your way through what is typically described as the “standard algorithm” for long division. More specifically, it is the traditional algorithm that has been taught in this country for decades. It goes without saying that virtually no student enjoys solving problems like these, and for most, we know this experience is more than frustrating.
Even worse, those who continue to fail at problems like these get even more of them in the effort to improve their skills through extra practice. The only relief for fourth or fifth grade students who finally succeed in doing multidigit long division problems is the algorithm disappears once they reach middle school and beyond.
In fairness, there is a reason for students to learn and use algorithms. They are reliable methods with repeated steps that lead to a correct answer. That is a core feature of mathematics. But if this is the case, then this goal can be accomplished with a variety of algorithms, and that is exactly what happens in different countries around the world.
There are three fundamental issues with the standard algorithm that make it frustrating and even misleading for students. First, the role of place value in the algorithm is lost and described incorrectly. In the example above, a teacher would commonly ask, “Can I divide 12 into 10? Can I divide 12 into 100?” This is incorrect for the simple reason that “10” in 1,008 is not 10, nor is the “100” in 1,008 actually 100.
Second, the algorithm is intense with procedural steps. There are more than 20 mental and written procedural steps needed to compute the answer to this problem. [“First I start with 12 into 100 (step 1), I determine that it goes in 8 times (step 2), write the 8 above the second 0 (step 3), etc.”] Make a mistake with any step, and the answer will almost assuredly be wrong.
The problem—and the core source of frustration for students—is that precise estimation skills are required. “Does 12 go into 100 six times? Seven times? Eight times? Nine times?” This kind of estimation is challenging to even the most proficient fourth and fifth grade students. Write and erase, write and erase. And yes, estimation is important, but it can also be taught in other contexts.
My deepest concern about requiring students to learn this algorithm for multidigit problems to the level of proficiency is time. Fifty years ago, schools didn’t have the range of standards nor the emphasis on conceptual understanding they do today. We don’t have the luxury of devoting most of a grade level to this kind of low-level mathematics.
The Partial Quotient Algorithm
As a math educator, I am often asked if “knowing your math facts” is still important in today’s world. Absolutely. A fluency in facts (12 x 3 = 36) and competence in what are called extended facts (12 x 30 = 360) allow students to devote their attention to other dimensions of a math problem. We use math facts all the time when we do multistep algebraic problems (and higher) so we can focus on the steps and strategies at each step to compute a final answer. This is simply an issue of efficient information processing.
A different approach for helping students move through and beyond multi digit long division is through the use of what we call the “facts toolbox” and the partial quotient algorithm. The teacher may begin the lesson by listing some known facts about multiples of 12 on the board. These are traditional “12 facts.” But some extended facts, as you can see, are also listed.
The key idea behind the partial quotient algorithm is students do not have to have the closest estimation when they begin solving the problem. You can see in Method 1 the student draws on facts and extended facts from the toolbox. The student starts with 12 x 50 = 600, writes the partial quotient of 50 above and the product 600 below, and then subtracts. From there, the algorithm cycles through repeated steps until there is nothing left to subtract1. You can also see the algorithm avoids the incorrect language of “12 divided into 10, 12 divided into 100…”
Method 2 is more sophisticated. The writing in the upper left shows the student is generating her own facts and extended facts. They are not part of the toolbox. Instead, the toolbox is merely a prompt to get the student to think of facts and extended facts on their own. Clearly, Method 2 leads to far fewer steps.

It is important students see different ways of solving the same problem. Comparisons between methods help develop strategic thinking in students. A pair of solutions can even be presented as “worked examples” before students solve other long division problems by themselves.
Over time, the toolbox can be faded from instruction, and students are simply encouraged to write off to the side of the problem possible relevant facts and extended facts if necessary.
The partial quotient method is widely cited in the current math education literature, particularly by Sybilla Beckmann2, one the members of the writing team for the Common Core Standards. In my opinion, it should replace the standard algorithm as it is taught in schools today.
References
1Long division problems should not contain remainders until students have learned about fractions. The traditional presentation of “r 3,” for example, is misleading because students tend to think of the remainder as a whole number rather than a fractional quantity.
2Beckmann, S. (2017). Mathematics for elementary teachers (5th Edition). Upper Saddle River, NJ: Pearson Education.

